PG: Progressão Geométrica

Página Inicial » Ensino Fundamental » Sequência » PG: Progressão Geométrica
PG ou progressão geométrica é uma sequência numérica onde os termos a partir do segundo são obtidos multiplicados por uma constante q que chamamos de razão.
Para encontrarmos a razão de uma PG basta dividirmos um número pelo seu antecessor.

Índice do Artigo

Exemplos de progressão geométrica

Considere as seguintes sequências geométricas:
  • (1, 2, 4, 8, 16, …) é uma P.G. crescente, com razão q = 2.
  • (5, 25, 125, 625, …) crescente, com razão q = 5.
  • (40, 20, 10, 5, 5⁄2, …) decrescente, com razão q = 1⁄2.
  • (2, -4, 8, -16, 32, …) oscilante, com razão q = -2.

Tipos de progressão geométrica

  • Crescente: onde cada termo da PG é maior que seu antecessor.Exemplo:
    • (1, 3, 9, 27, …) com q = 3
    • (-2, -1, –1⁄2, –1⁄4, …) com q = 1⁄2
  • Decrescente: onde cada termo da P.G. é menor que seu antecessor. Exemplo:
    • (-1, -4, -16, -64, …) com q = 4
    • (2, 1, 1⁄2, 1⁄4, 1⁄8, …) com q = 1⁄2
  • Constante: quando o próximo termo, a partir do segundo, é uma sequencia de números iguais, isso acontece quando q = 1.Exemplo:
    • (2, 2, 2, 2, 2, …) com q = 1
  • Oscilante: quando o próximo termo, a partir do segundo, é um número negativo. Isto acontece quando a razão é negativa, ou seja, q < 0.Exemplo:
    • (2, -4, 8, -16, 32, -64, …) com q = -2

Termo geral de uma PG

Podemos encontrar qualquer termo geral de uma PG ou o total de termos da seguinte forma:
Seja a PG com razão q a seguir:
  • (a1, a2, a3, …, an, …)
A partir da sequência acima sabemos que:
  • a2 = a1 . q
  • a3 = a2 . q
  • a4 = a3 . q
  • a5 = a4 . q
  • …
  • an = an-1 . q
Se multiplicarmos as igualdades acima, membro a membro, teremos:
(a2 . a3 . a3 . … . an-1) . an = a1 . (a2 . a3 . … an-1) . q . q . q . … + q ((n – 1) vezes)
Após simplificarmos os termos, chegamos a fórmula:
  • an = a1 . q(n – 1)
Onde:
  • an: é o termo geral da PG;
  • a1: é o primeiro termo;
  • n: é o número de termos ou o total de termos;
  • q: é a razão.
Exemplo:
  1. Determine o 5º (quinto) termo de uma PG sabendo que a1 = 3 e q = 4.Para isso vamos utilizar a fórmula geral. Veja!
    De acordo com o enunciado temos que: a1 = 3, q = 4 e n = 5Assim:
    a5 = 3 x 4(5 – 1)a5 = 3 x 44
    a5 = 3 x 256a5 = 768
    Vamos conferir: 3, 12, 48, 192, 768, … Correto!

Soma dos n termos de uma PG finita

Podemos encontrar a soma dos n os termos de uma progressão geométrica a partir da fórmula geral.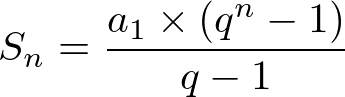
Soma dos n termos de uma PG: progressão geométrica finita
Exemplo:
Considere a PG: (2, 6, 18, …), calcule os 5 primeiros termos.
Temos que a1 = 2, q = 3 e n = 5
Logo,
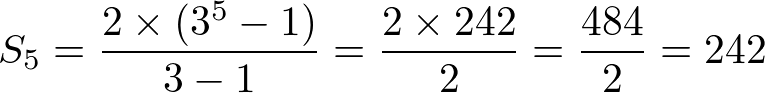
Soma dos n termos de uma PG: progressão geométrica finita

Soma dos infinitos termos de uma PG

É possível somar os termos de uma progressão geométrica infinita. Podemos fazer isso quando os termos de uma PG acabe convergindo para o valor 1. Isso ocorre quando a razão q for um número entre -1 e 1.
Logo, quando n tende ao infinito, temos a seguinte fórmula para a soma dos infinitos termos:
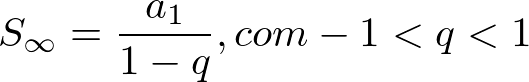
Soma dos infinitos termos de uma P.G.
Exemplo:
Calcule o valor para x = 1 + 1⁄3 + 1⁄9 + …
O valor de x é a soma dos infinitos termos da PG: (1 + 1⁄3 + 1⁄9 + …)
Assim:
a1 = 1 e q = 1⁄3
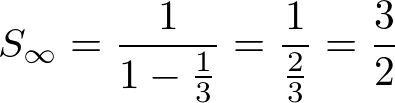
Soma dos infinitos termos de uma P.G.

Produto dos n termos de uma PG

Também é possível fazer o produto dos n termos de uma PG, para isso a seguinte fórmula pode ser usada: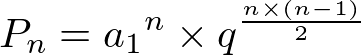
Produto dos n termos de uma P.G.
Onde:
  • Pn: é o produto dos n termos;
  • n: é o número total de termos;
  • a1: é o primeiro termo.

Propriedade

  • Cada termo de uma PG, a partir do segundo, é a média geométrica entre o sucessor e antecessor. Então, seja a PG (a, b, c, …), temos que: b² = a.c
Veja mais…
Progressão Aritmética
Tabuada
Razão e Proporção
Encontrou algum erro? Nos avise clicando aqui
Authorby Jean Carlos Novaes